Decimal Number System
Return to the numbers pages | Decimal Numbers | Binary Numbers | Hexadecimal Numbers | Octal Numbers | BCD Number | Negative Numbers | Number ConversionsThe decimal number system is the number system we use everyday, from counting to simple math like checking store recepts.
The word 'deci' means 10, therefore there are ten numbers (digits) in the decimal decimal number system. The valid numbers in a base 10 number system are:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
All number systems have a 'base'. The base is the same as the number of valid numbers in the system. Since the decimal number system has 10 valid numbers it is a 'base 10' number system. The base is also referred to as a 'radix' and in the PLC/PAC software the user can change the radix (base) of the numbers for display purposes.
A decimal number showing its base would be written:
25710 or 257d
Where the small letter 'd' designates that it it a decimal number. We normally do not write the base on decimal numbers. If the base is not displayed the number is assumed to be a decimal number.
Digit Weighting
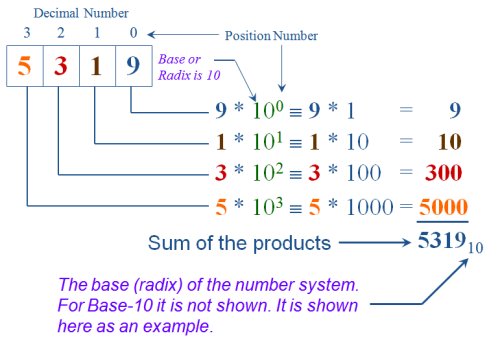
Each digit in a number system has a weight value assigned. Decimal numbers are 'base-10' numbers, therefore the weight of each digit is a power of 10.
Each digit also has a position number. The first digit on the right is position zero. The next digit to the left is position one. To the left again is position two, etc.
The weight of the digit in each position is the base of the number system raised to the power of the position number. The value of the number is than calculated by multiplying the value of the digit in each position by the base raised to the power of that position and then summing the products.
The following figure represents a decimal number with the position and weight of each digit shown and how the value of the number is derived.